📌 What is a Number?
A number is a mathematical object used to count, measure, and label. It helps us understand quantity, order, and value.
📊 Classification of Numbers:
Here’s a simple diagram showing the Types Of Numbers in maths:
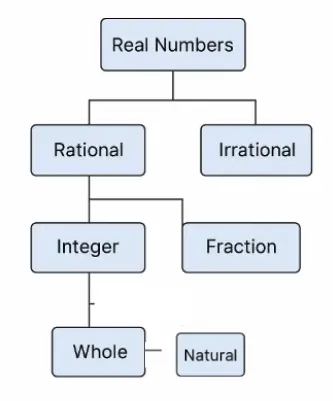
📚 Types Of Numbers in Maths (With Definitions):
| Type of Number | Symbol | Definition | Examples |
|---|---|---|---|
| Natural Numbers | N | Counting numbers starting from 1 | 1, 2, 3, 4, … |
| Whole Numbers | W | Natural numbers including 0 | 0, 1, 2, 3, … |
| Integers | Z | Whole numbers and their negatives | -3, -2, 0, 1, 2 |
| Rational Numbers | Q | Numbers expressed as p/q, q ≠ 0 | 1/2, 3, -4, 0.75 |
| Irrational Numbers | – | Cannot be expressed as p/q, non-repeating, non-terminating decimals | √2, π, e |
| Real Numbers | R | All rational and irrational numbers | -2, 0, 4.5, π |
| Imaginary Numbers | i | Square root of negative numbers | √-1 = i, 2i |
| Complex Numbers | C | Numbers having real and imaginary parts | 3 + 2i, -1 – i |
🧮 Number System Formula (Quick Recap):
Here are a few formulas and properties to remember:
- Sum of first n natural numbers:
S = n(n + 1)/2 - Sum of first n odd natural numbers:
S = n² - Sum of first n even natural numbers:
S = n(n + 1) - Property of Rational Number:
If a number can be written as p/q (where p, q ∈ Z and q ≠ 0), it is rational.
🎯 Examples for Better Understanding:
Let’s break down a few numbers:
| Number | Type(s) It Belongs To |
|---|---|
| 5 | Natural, Whole, Integer, Rational, Real |
| 0 | Whole, Integer, Rational, Real |
| -3 | Integer, Rational, Real |
| 4/7 | Rational, Real |
| √2 | Irrational, Real |
| π | Irrational, Real |
| 3 + 2i | Complex (Not a real number) |
✍️ Why You Should Learn Types Of Numbers in Maths:
Understanding different types of numbers is vital because:
- It helps in competitive exams like WBCS, SSC, UPSC, Banking, etc.
- It forms the basis for algebra, geometry, and arithmetic.
- It’s crucial for data interpretation and logical reasoning.
📝 Practice Questions:
Q1) Which of the following is an irrational number?
- 7
- 22/7
- √5
- 0.5
Ans: 3) √5
Q2) What type of number is -4?
- Natural
- Integer
- Whole
- Irrational
Ans: 2) Integer
Q3) Which of these numbers is not a rational number?
- 1/2
- 3
- √2
- -7
Ans: 3) √2
Q4) Identify the complex number:
- 5
- 2 + 3i
- -4
- 1/2
Ans: 2) 2 + 3i
Q5) Which number is both an integer and a rational number?
- 3
- √3
- π
- 2i
Ans: 1) 3
🧠 Trick to Remember Number Types:
- Natural – Starts at 1
- Whole – Natural + 0
- Z Integers – Includes negatives
- Q Rational – Fraction form
- Irrational – Weird decimals
- R Real – Rational + Irrational
- C Complex – Real + Imaginary
📝 Tip: Think of it like N ⊂ W ⊂ Z ⊂ Q ⊂ R ⊂ C
🧑🏫 Real-Life Examples:
- Your age = Natural number
- Bank balance = Rational or Integer
- Length of diagonal of a square = Irrational (like √2)
- AC electricity = Uses complex numbers
- Coding & Computers = Use binary number system (another type!)
📌 Summary Table:
| Symbol | Type | Includes |
|---|---|---|
| N | Natural | 1, 2, 3, … |
| W | Whole | 0, 1, 2, … |
| Z | Integers | -3, -2, 0, 1, 2 |
| Q | Rational | p/q, q ≠ 0 |
| – | Irrational | π, √2, e |
| R | Real | Rational + Irrational |
| i | Imaginary | √-1, 2i |
| C | Complex | a + bi |
✨ Final Thoughts:
The Types Of Numbers in maths is one of the first things students learn, and it’s a base for everything in math. Whether you are preparing for exams or brushing up on basics, mastering this concept is a must.
We hope this guide helped you understand the Types Of Numbers in number system in a clear and structured way.
**You Might Also Like:
- Must-Know Algebra Formulas for Competitive Exams with Examples & Questions
- Percentage Important Concepts
- Percentage Formula & Shortcut Tricks for Exams
Download PDF Version
To get a printable “Algebra Formulas for Competitive Exams PDF”, Click Here and revise anytime!







