📘 What is Trigonometry?
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of a right-angled triangle. The word ‘trigonometry’ is derived from the Greek words trigonon (triangle) and metron (measure).
In Class 10, the focus is primarily on:
- Understanding trigonometric ratios
- Using identities and formulas
- Solving triangles
- Applying these in real-life and word problems
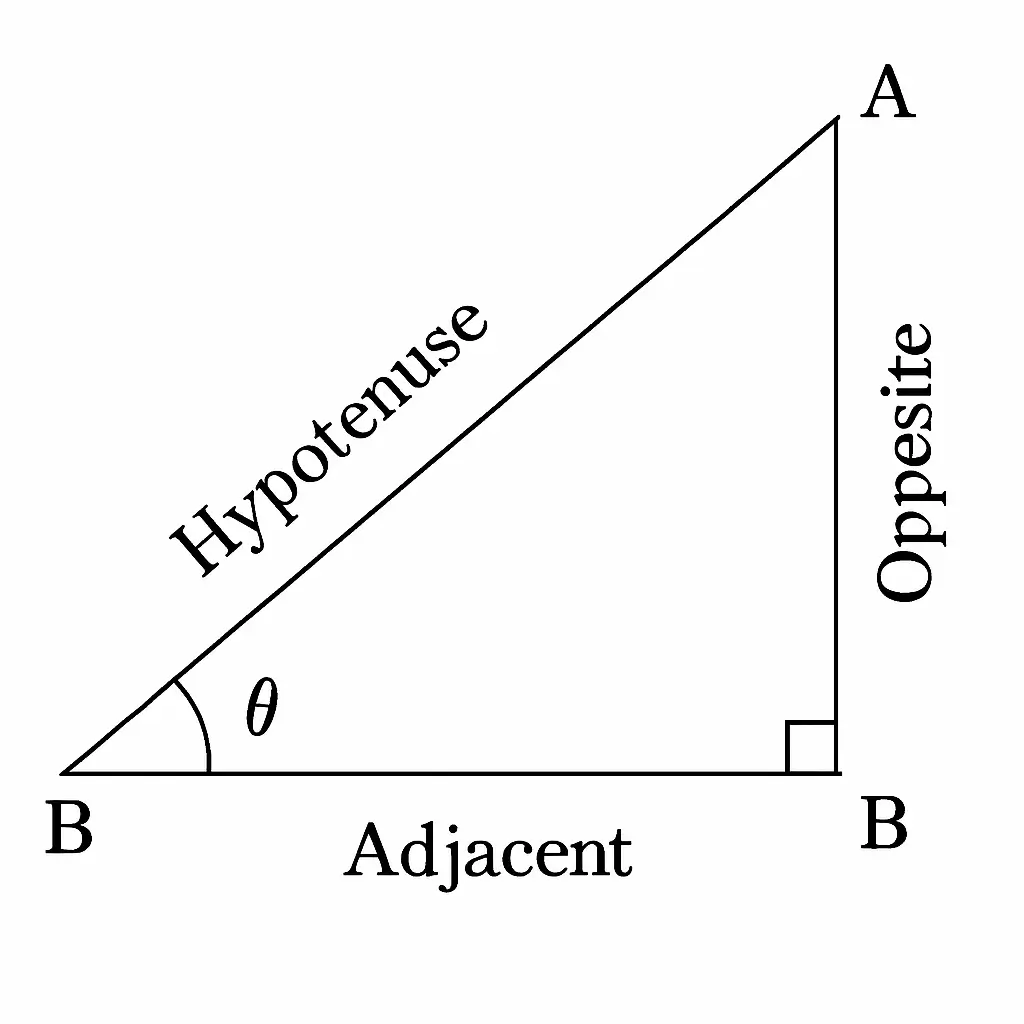
🔢 Trigonometric Ratios Table (Basic):-
The six basic trigonometric ratios are:
| Ratio | Formula | Explanation |
|---|---|---|
| sin θ | Opposite side / Hypotenuse | Vertical / Slant |
| cos θ | Adjacent side / Hypotenuse | Base / Slant |
| tan θ | Opposite side / Adjacent side | Vertical / Base |
| cosec θ | Hypotenuse / Opposite side | 1 / sin θ |
| sec θ | Hypotenuse / Adjacent side | 1 / cos θ |
| cot θ | Adjacent side / Opposite side | 1 / tan θ |
🧠 Memory Tip: SOH-CAH-TOA:-
To remember the trigonometric ratios easily, use:
SOH – Sin = Opposite / Hypotenuse
CAH – Cos = Adjacent / Hypotenuse
TOA – Tan = Opposite / Adjacent
📊 Trigonometric Ratios of Standard Angles:-
| Angle (θ) | sin θ | cos θ | tan θ | cosec θ | sec θ | cot θ |
|---|---|---|---|---|---|---|
| 0° | 0 | 1 | 0 | Not defined | 1 | Not defined |
| 30° | 1/2 | √3/2 | 1/√3 | 2 | 2/√3 | √3 |
| 45° | 1/√2 | 1/√2 | 1 | √2 | √2 | 1 |
| 60° | √3/2 | 1/2 | √3 | 2/√3 | 2 | 1/√3 |
| 90° | 1 | 0 | Not defined | 1 | Not defined | 0 |
🧮 Important Trigonometry Formulas for Class 10:-
Here are the most used trigonometry formulas for Class 10:
✅ Reciprocal Identities:-
- cosec θ = 1 / sin θ
- sec θ = 1 / cos θ
- cot θ = 1 / tan θ
✅ Quotient Identities:-
- tan θ = sin θ / cos θ
- cot θ = cos θ / sin θ
✅ Pythagorean Identities:-
- sin²θ + cos²θ = 1
- 1 + tan²θ = sec²θ
- 1 + cot²θ = cosec²θ
📐 Pythagorean Theorem – Definition & Formula:-
The Pythagorean Theorem is a fundamental relation between the sides of a right-angled triangle. It is the foundation of many trigonometric concepts taught in Class 10.
🔷 Statement:
In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
🔢 Formula:
Hypotenuse² = Base² + Height²
Or in simple terms:
c² = a² + b²
Where:
- c = hypotenuse (longest side, opposite the right angle)
- a and b = the two other sides (base and height)
🖼️ Diagram of Pythagorean Theorem:-
Here is a visual diagram of a right-angled triangle applying the Pythagorean Theorem:

✏️ Example 1
Q: In a right triangle, the base is 6 cm and the height is 8 cm. Find the hypotenuse.
Solution:
Base = 6 cm
Height = 8 cm
Using the formula:
Hypotenuse² = 6² + 8² = 36 + 64 = 100
Hypotenuse = √100 = 10 cm
✏️ Example 2
Q: A ladder is placed against a wall. It reaches 12 meters high on the wall and is 5 meters away from the wall at the base. Find the length of the ladder.
Solution:
This forms a right-angled triangle:
Height = 12 m, Base = 5 m
Length of ladder = Hypotenuse
Hypotenuse² = 12² + 5² = 144 + 25 = 169
Hypotenuse = √169 = 13 m
🧠 Pythagorean Theorem in Trigonometry:-
The Pythagorean identity in trigonometry is derived from this theorem:
sin²θ + cos²θ = 1
It shows the same relationship between the perpendicular and base relative to the hypotenuse in a unit circle or right triangle.
📝 Practice Questions (With Answers):-
- The sides of a triangle are 5 cm and 12 cm. Find the hypotenuse.
- Answer: √(5² + 12²) = √169 = 13 cm
- A tree is broken and the top touches the ground 15 meters away. If the broken part is 20 meters long, find the height from which the tree broke.
- Answer: √(20² – 15²) = √175 = ≈13.2 m
- If the hypotenuse of a right triangle is 17 cm and one side is 8 cm, find the other side.
- Answer: √(17² – 8²) = √(289 – 64) = √225 = 15 cm
📘 Applications of Trigonometry in Real Life:-
Even though it looks theoretical, trigonometry has real-life uses in:
- Measuring heights and distances
- Construction and architecture
- Navigation and GPS
- Astronomy
In Class 10, questions often revolve around finding the height of a tree or a building using trigonometric ratios based on angles of elevation or depression.
🧠 Examples of Trigonometry Problems:-
Example 1: If sin θ = 3/5, find cos θ and tan θ.
Solution:
Given, sin θ = Opposite / Hypotenuse = 3/5
Using Pythagoras:
Adjacent = √(5² – 3²) = √(25 – 9) = √16 = 4
So,
cos θ = 4/5
tan θ = 3/4
Example 2: If tan A = 1, find the value of sin²A + cos²A.
Solution:
We know:
sin²A + cos²A = 1 (Always true for any angle)
So, the answer is 1
Example 3: Find the value of: sin 30° * cos 60° + cos 30° * sin 60°
Solution:
= (1/2)(1/2) + (√3/2)(√3/2)
= 1/4 + 3/4 = 1
✍️ Practice Questions:-
Try these questions on your own to test your understanding:
- If cos θ = 5/13, find sin θ and tan θ.
- Prove: sin²A + cos²A = 1
- Find the value of: tan 45° + cot 45°
- If tan A = √3, find sin A and cos A.
- A ladder 10 m long is leaning against a wall making an angle of 60° with the ground. Find the height it reaches on the wall.
📥 Trigonometry Formulas for Class 10 PDF Download:-
To make your revision easier, we have compiled all important trigonometry formulas for Class 10 in a PDF format. This handy document is great for last-minute revisions and offline study.
Click below to get your Trigonometry Formulas for Class 10 PDF Download: 🔽 [Download PDF]
This PDF includes:
- All essential formulas
- Standard angles chart
- Identities
- Reciprocal, quotient and Pythagorean formulas
Make sure to print and stick it on your study wall!
🎯 Tips to Master Trigonometry in Class 10:-
- Understand the triangle and label sides correctly.
- Memorize trigonometric ratios and formulas regularly.
- Practice questions involving angles of elevation and depression.
- Revise standard angles table often.
- Download and keep the trigonometry formulas for Class 10 PDF download handy.
🧾 Conclusion:-
Trigonometry may seem tough at first, but with consistent practice and clear understanding of the formulas, it becomes a scoring topic. Focus on understanding the logic behind each ratio, apply them in problems, and revise using the trigonometry formulas for Class 10 PDF download we’ve provided above.
Happy Learning! 📚






