Understand the basic concept of ratio and proportion aptitude with clear definitions, real-life examples, and practice questions. Perfect for competitive exams.
01) What is Ratio?
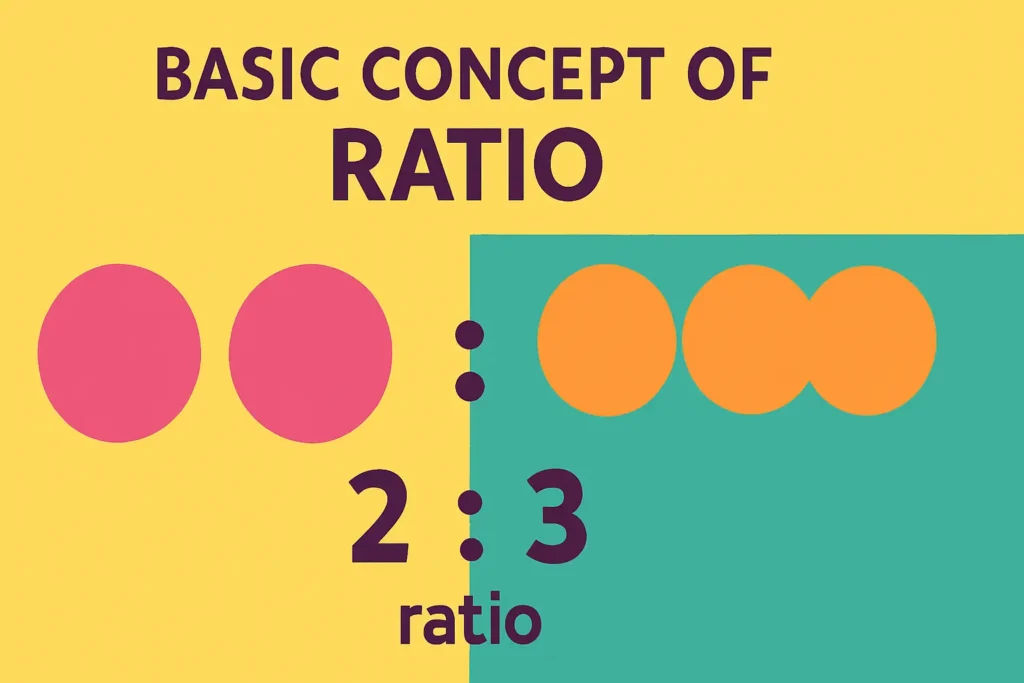
A ratio is a way to compare two quantities of the same kind by division. It shows how many times one quantity is contained in another.
Example:
If the age of Ram is 20 years and Shyam is 30 years, then the ratio of their ages is:
20:30 = 2:3
This means for every 2 years of Ram, Shyam has 3 years.
02) Key Points about Ratio:
- It has no unit.
- It is always written in simplest form.
- Order matters. (Ratio of A to B is different from B to A)
03) Types of Ratios in Ratio and Proportion Aptitude:
Understanding the different types of ratios helps in solving a variety of ratio and proportion aptitude questions with clarity. Here are the most important types:
1. Simple Ratio:
A simple ratio is the direct comparison between two quantities of the same kind.
Example:
If there are 6 boys and 4 girls in a class, the ratio of boys to girls is:
6:4 = 3:2
This is a simple form and most commonly used in ratio and proportion aptitude problems.
2. Compound Ratio:
A compound ratio is formed by multiplying two or more ratios.
Example:
If the first ratio is 2:3 and the second is 4:5,
then the compound ratio = (2×4):(3×5) = 8:15
Compound ratios are often used in advanced level aptitude questions.
3. Inverse Ratio (Reciprocal Ratio):
In inverse ratio, we simply reverse the terms of a given ratio.
Example:
If the ratio is 3:5, the inverse ratio is 5:3
It’s used when two quantities are inversely related. For example, if the number of workers increases, the time taken decreases.
4. Duplicate Ratio:
The duplicate ratio is the square of the terms in a given ratio.
Example:
If the ratio is 2:3, then the duplicate ratio is:
(2²):(3²) = 4:9
This type is useful in geometry-based and algebraic ratio problems.
5. Triplicate Ratio:
The triplicate ratio is the cube of the terms in a given ratio.
Example:
If the ratio is 2:3, the triplicate ratio is:
(2³):(3³) = 8:27
6. Sub-Duplicate Ratio:
The sub-duplicate ratio is the square root of each term in a ratio.
Example:
If the ratio is 4:9, the sub-duplicate ratio is:
√4 : √9 = 2:3
7. Sub-Triplicate Ratio:
The sub-triplicate ratio is the cube root of each term.
Example:
If the ratio is 8:27, the sub-triplicate ratio is:
∛8 : ∛27 = 2:3
8. Equal Ratio:
Two or more ratios are said to be equal if their cross products are equal.
Example:
If 2:3 = 4:6, then
2 × 6 = 12 and 3 × 4 = 12
Since cross products are equal, the ratios are equal ratios.
This concept is widely used in proportion problems.
04) What is Proportion?

Proportion is an equation that shows two ratios are equal.
Example:
If 2:3 = 4:6, then we say that the four numbers are in proportion.
That is, 2:3 :: 4:6 or 2/3 = 4/6
05) Types of Proportion in Ratio and Proportion Aptitude:
In ratio and proportion aptitude, understanding how quantities are related is key. There are two main types of proportion you’ll often encounter in exams:
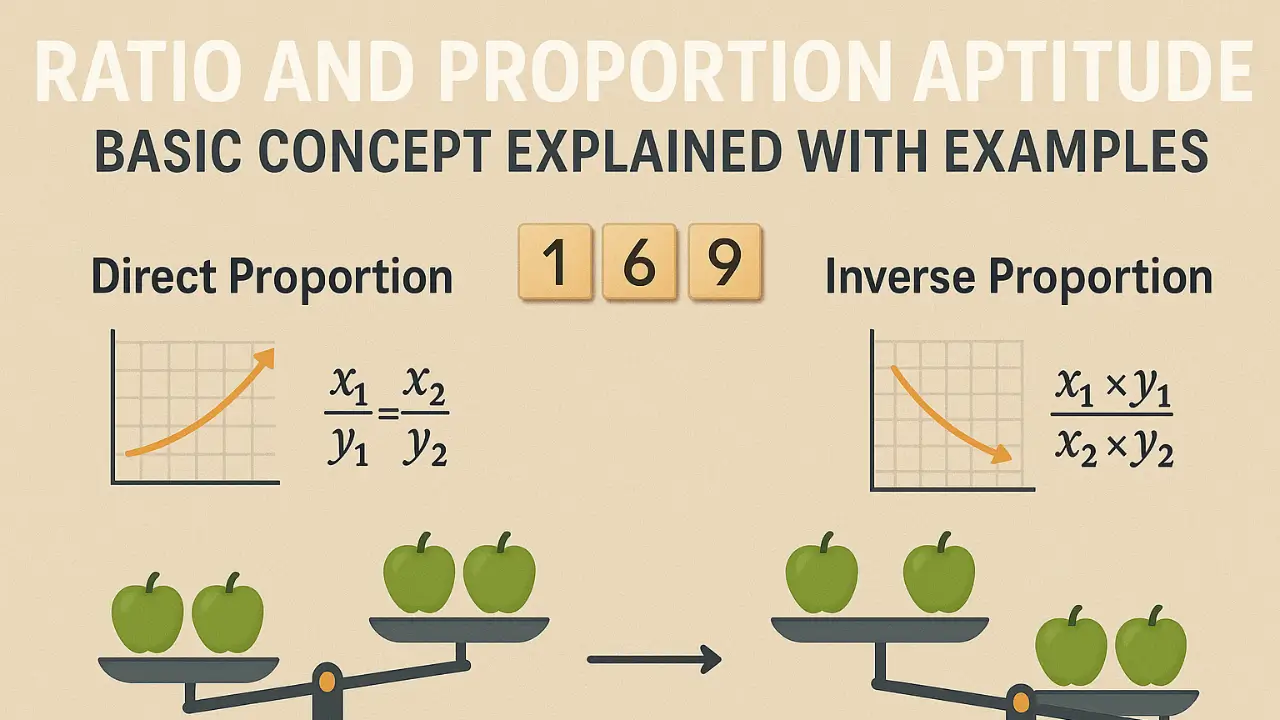
1. Direct Proportion:
In direct proportion, as one quantity increases, the other also increases in the same ratio. Likewise, if one decreases, the other also decreases proportionally.
✅ Real-Life Example:
Let’s say you buy mangoes at ₹50 per kg.
- If you buy 2 kg, the cost is ₹100.
- If you buy 4 kg, the cost becomes ₹200.
More mangoes → More cost.
Less mangoes → Less cost.
This is direct proportion.
✅ Formula:
If x₁/x₂ = y₁/y₂, then the quantities are in direct proportion.
✅ Example Question (Aptitude Style):
Question: If 6 pens cost ₹60, how much will 10 pens cost?
Solution:
6 pens → ₹60
1 pen → ₹10
So, 10 pens = 10 × 10 = ₹100
Or use direct proportion:
6/60 = 10/x
Cross-multiplying:
6x = 600 → x = ₹100
2. Inverse Proportion:
In inverse proportion, as one quantity increases, the other decreases, and vice versa. The product of the two quantities remains constant.
✅ Real-Life Example:
You need to complete a task in 12 hours with 4 workers.
Now, if you increase the number of workers to 6, the work will be done faster.
More workers → Less time.
This is inverse proportion.
✅ Formula:
If x₁ × y₁ = x₂ × y₂, then the quantities are in inverse proportion.
✅ Example Question (Aptitude Style):
Question: If 4 men can complete a task in 12 days, how many days will 6 men take?
Solution:
More men → fewer days. So, use inverse proportion:
4 × 12 = 6 × x
48 = 6x → x = 8 days
So, 6 men will finish the work in 8 days.
06) Ratio and Proportion Aptitude Examples:
Let’s understand the concept through simple examples:
Example 1:
Divide ₹1800 between A and B in the ratio 2:1.
Solution:
Total parts = 2 + 1 = 3
A’s share = (2/3) × 1800 = ₹1200
B’s share = (1/3) × 1800 = ₹600
Example 2:
If 3 pens cost ₹45, what is the cost of 5 pens?
Solution:
This is a case of direct proportion.
More pens = more cost.
Let x be the cost of 5 pens.
Then, 3/45 = 5/x
Cross-multiplying: 3x = 225 → x = ₹75
07) Why Ratio and Proportion Aptitude is Important for Exams:
- It forms the base of many quantitative aptitude chapters like Partnership, Mixture, Time-Work, etc.
- Questions are easy and scoring.
- Quick tricks and proper understanding can save time.
08) Ratio and Proportion Aptitude – Practice Questions:
Question 1:
The ratio of two numbers is 4:5. If the sum is 72, find the numbers.
A) 36 and 36
B) 32 and 40
C) 40 and 32
D) 28 and 44
Question 2:
If a : b = 3 : 4 and b : c = 2 : 5, find a : c.
A) 3 : 10
B) 6 : 20
C) 3 : 5
D) 6 : 15
Question 3:
₹1500 is divided among A, B, and C in the ratio 2:3:5. What is C’s share?
A) ₹500
B) ₹750
C) ₹600
D) ₹900
09) Answers and Solutions:
Answer 1: B) 32 and 40
Explanation:
The ratio of two numbers is 4:5
Sum of ratio parts = 4 + 5 = 9
Each part = 72 ÷ 9 = 8
So, the numbers are 4×8 = 32 and 5×8 = 40
Answer 2: A) 3 : 10
Explanation:
a : b = 3 : 4
b : c = 2 : 5
To link both ratios, make the common term (b) equal.
LCM of 4 and 2 = 4
a : b = 3 : 4 (no change)
b : c = 2 : 5 → multiply both terms by 2 → 4 : 10
Now, a : c = 3 : 10
Answer 3: B) ₹750
Explanation:
Total ratio = 2 + 3 + 5 = 10 parts
C’s share = (5/10) × ₹1500 = ₹750
10) Conclusion:
The basic understanding of ratio and proportion aptitude will help you solve many types of math questions easily in your competitive exams. Keep practicing different question patterns and revise the concepts regularly. With clear fundamentals and daily practice, you can master this topic confidently.
Want To Practice More Questions On Ratio and Proportion Aptitude?
👉 Ratio and Proportion Aptitude Questions Practice Sets
**You Might Also Like:
- Must-Know Algebra Formulas for Competitive Exams with Examples & Questions
- Percentage Important Concepts
- Simple Interest Practice Questions Set 01 – For Govt Job & Academic Exams
Follow Us on Facebook:
Stay updated with the latest math practice sets, tips, and exam strategies. Follow Mathsmine on Facebook for Daily Updates