Learn all important lines and angles formulas with simple explanations, solved examples, and practice questions. Perfect for competitive exams like SSC, Railways, Banking, and more.
01) What are Lines and Angles?
Before jumping into the formulas, let’s understand the basics.
- A line is a straight path that extends in both directions with no endpoints.
- A ray is a line with one endpoint.
- An angle is formed when two rays meet at a common endpoint called the vertex.
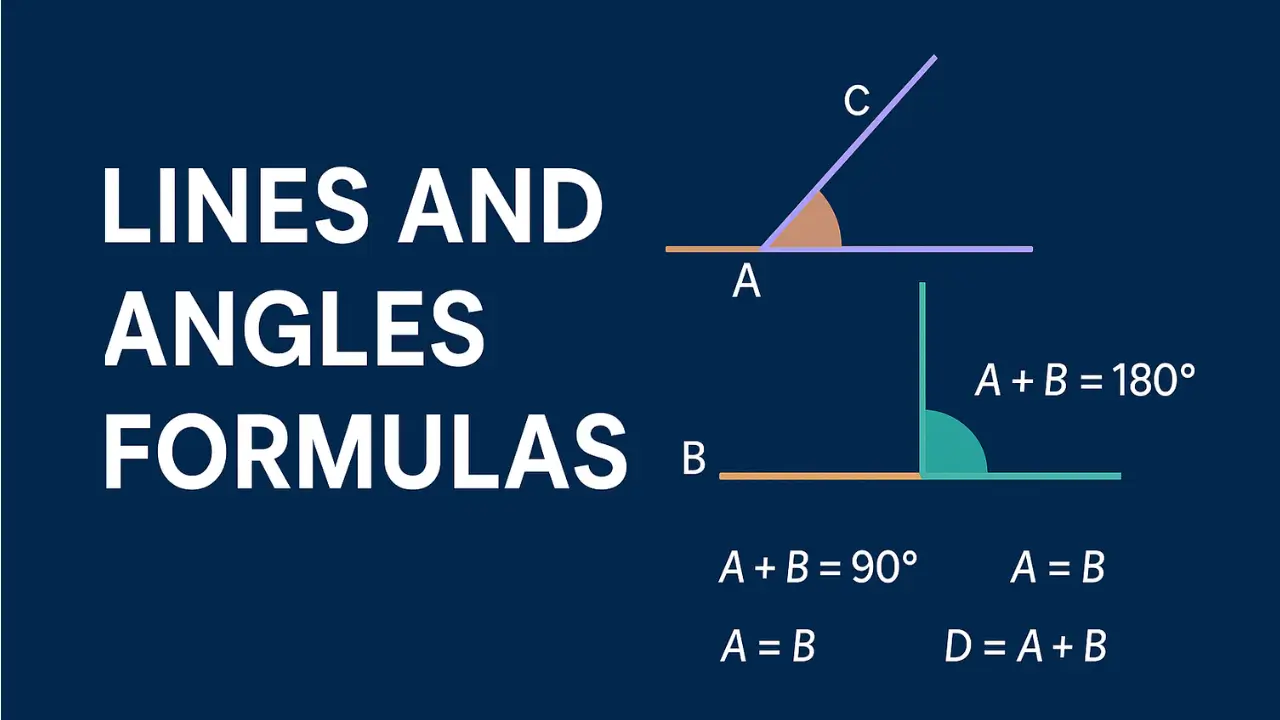
02) Important Lines and Angles Formulas:
Here are some essential lines and angles formulas that you need to remember for solving problems:
| Type of Angle | Formula / Rule |
|---|---|
| Complementary Angles | Sum = 90° → A + B = 90° |
| Supplementary Angles | Sum = 180° → A + B = 180° |
| Linear Pair of Angles | Formed on a straight line → A + B = 180° |
| Vertically Opposite Angles | Always equal → A = B |
| Adjacent Angles | Share a common arm and vertex |
| Angle at a point | Sum of angles around a point = 360° |
| Corresponding Angles | Equal when two lines are parallel |
| Alternate Interior Angles | Equal when two lines are parallel |
| Co-Interior Angles | Supplementary → A + B = 180° |
| Angle Sum of Triangle | A + B + C = 180° |
| Exterior Angle of Triangle | Equal to sum of two opposite interior angles → D = A + B |
These are the most used lines and angles formulas in exam questions.
03) Shortcut Tricks to Remember:
- Linear pair always adds up to 180°.
- If two angles are vertically opposite, they are always equal.
- In parallel lines, corresponding and alternate angles are equal.
- In a triangle, exterior angle = sum of two remote interior angles.
04) Examples with Solutions:
Let’s apply the lines and angles formulas to solve some real exam-style questions.
Example 1:
Question: Two angles form a linear pair. One angle is 70°. Find the other.
Solution:
Linear pair → A + B = 180°
So, 70° + B = 180°
⇒ B = 180° – 70° = 110°
Example 2:
Question: Two complementary angles differ by 20°. Find the angles.
Solution:
Let the smaller angle = x
Then the other angle = x + 20
x + x + 20 = 90 → 2x = 70 → x = 35
Other angle = 55
Answer: 35° and 55°
Example 3:
Question: Find the value of the angle vertically opposite to 60°.
Solution:
Vertically opposite angles are equal.
Answer: 60°
Example 4:
Question: Two parallel lines are cut by a transversal. One of the alternate interior angles is 65°. Find the other.
Solution:
Alternate interior angles are equal.
Answer: 65°
05) Practice Questions:
Try solving these questions yourself using the lines and angles formulas we discussed above.
| Question | Options |
|---|---|
| 1. What is the supplement of 112°? | a) 68° b) 78° c) 88° d) 92° |
| 2. If two angles are complementary and one is 47°, find the other. | a) 53° b) 43° c) 33° d) 73° |
| 3. If one angle of a linear pair is 120°, find the other. | a) 60° b) 70° c) 80° d) 90° |
| 4. Vertically opposite angle of 135° is? | a) 135° b) 145° c) 125° d) 130° |
| 5. If the exterior angle of a triangle is 100°, and one interior opposite angle is 40°, find the other. | a) 60° b) 50° c) 45° d) 55° |
06) Answers with Solutions:
- a) 68°
Supplement = 180 – 112 = 68° - a) 43°
Complement = 90 – 47 = 43° - a) 60°
Linear pair = 180 – 120 = 60° - a) 135°
Vertically opposite = same angle - b) 60°
Exterior angle = sum of opposite interior angles
100 = 40 + x ⇒ x = 60
07) Chart Summary of Angles:
| Angle Type | Definition | Example Value |
|---|---|---|
| Acute Angle | Less than 90° | 45°, 60°, etc. |
| Right Angle | Exactly 90° | 90° |
| Obtuse Angle | Between 90° and 180° | 120°, 135° |
| Straight Angle | Exactly 180° | 180° |
| Reflex Angle | Between 180° and 360° | 250°, 300° |
| Full Rotation Angle | Exactly 360° | 360° |
08) Final Tips:
- Make flashcards of all the lines and angles formulas and revise them daily.
- Practice questions from previous year papers to understand question patterns.
- Draw diagrams while solving problems—it helps visualize the angles better.
Whether it’s solving SSC CGL, Railway NTPC, or Banking prelims, mastering lines and angles formulas gives you an edge in geometry questions.
Keep practicing, and soon you’ll solve these in seconds!
**You Might Also Like:
- Must-Know Algebra Formulas for Competitive Exams with Examples & Questions
- Percentage Practice Questions With Answers
- Percentage Formula & Shortcut Tricks for Exams
Download PDF Version
To get a printable “Algebra Formulas for Competitive Exams PDF”, click here and revise anytime!