Whether you’re preparing for a competitive exam, a school test, or simply brushing up your math skills, this guide will make calculating the area of an equilateral triangle feel like a breeze!
📘 What is an Equilateral Triangle?
An equilateral triangle is a special type of triangle in which:
- All three sides are equal in length.
- All three angles are equal, and each measures 60°.
✅ Properties of an Equilateral Triangle:
| Property | Value/Explanation |
|---|---|
| Number of sides | 3 |
| Length of all sides | Equal |
| Measure of all angles | 60° |
| Symmetry | 3 lines of symmetry |
| Area Formula | (√3 / 4) × a² |
🧮 Formula for the Area of an Equilateral Triangle:
The standard area of an equilateral triangle with side length a is:
👉 Area = (√3 / 4) × a²
Where:
- a = length of the side
- √3 ≈ 1.732
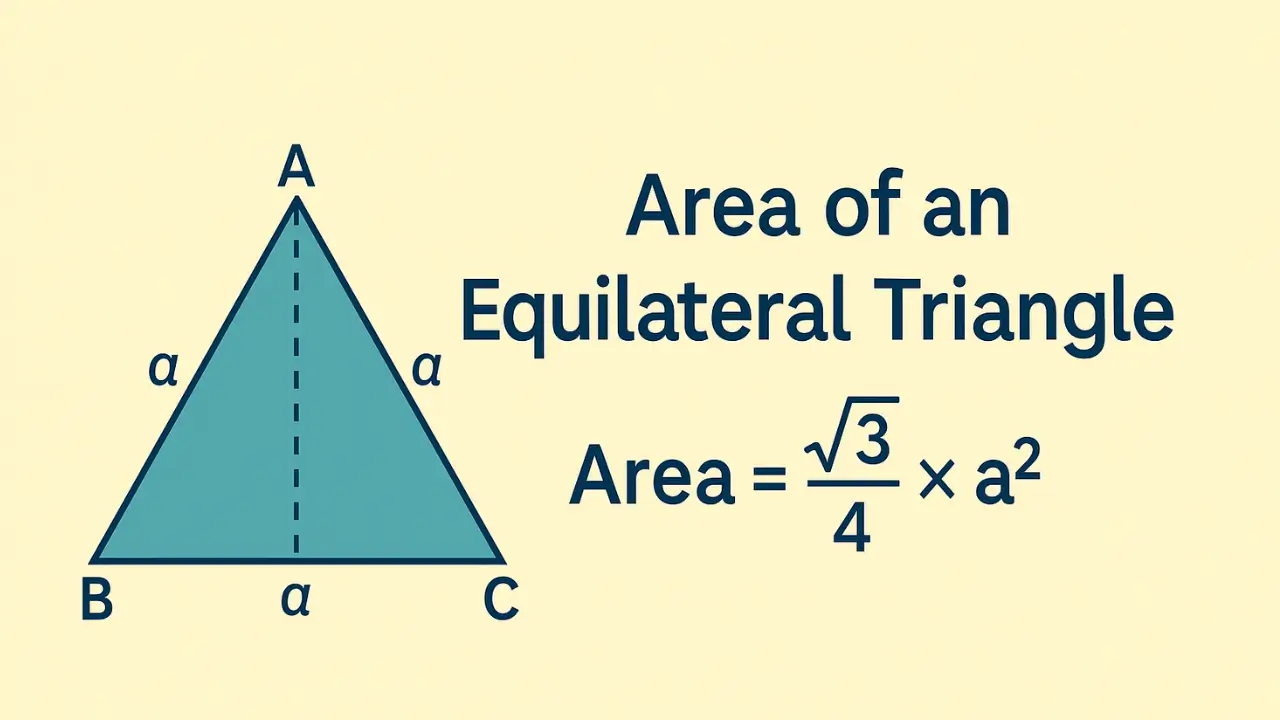
📊 Visual Understanding – Diagram:
Here’s a diagram to help visualize the components:
A
/ \
/ \
/ \
/ \
B---------C
Let all sides AB = BC = CA = a
Height is drawn from A to the base BC, say D
- BD = DC = a/2
- Using Pythagoras:
AD=a2−(a/2)2=3a2/4=(3/2)×aAD = \sqrt{a^2 – (a/2)^2} = \sqrt{3a^2/4} = (\sqrt{3}/2) × aAD=a2−(a/2)2=3a2/4=(3/2)×a
So,
Area = ½ × base × height = ½ × a × (√3/2 × a) = (√3/4) × a²
🧠 Why This Formula Works?
The logic behind the formula lies in splitting the triangle into two right-angled triangles and using the Pythagorean theorem. Since the base is divided into two equal parts and the height is calculated using Pythagoras, it naturally leads to the derived formula.
💡 Real-Life Application:
Equilateral triangles are seen in:
- Architectural designs
- Tiling patterns
- Traffic signs
- Structural frames (because of equal force distribution)
Knowing the area of an equilateral triangle helps in calculating surface area, construction planning, and in competitive exams like SSC, WBCS, UPSC, and Railways.
📘 Example 1: Basic Calculation:
Q. Find the area of an equilateral triangle with side length 6 cm.
Solution:
Area = (√3 / 4) × a²
= (√3 / 4) × 6²
= (√3 / 4) × 36
= 9√3 cm² ≈ 15.588 cm²
📘 Example 2: Word Problem:
Q. A decorative tile is shaped like an equilateral triangle with a side of 10 cm. What is its area?
Solution:
Area = (√3 / 4) × a²
= (√3 / 4) × 10²
= (√3 / 4) × 100
= 25√3 cm² ≈ 43.3 cm²
📐 Chart – Side vs. Area of an Equilateral Triangle:
| Side Length (a) | Area (Exact) | Area (Approx) |
|---|---|---|
| 2 cm | (√3/4) × 4 = √3 | 1.732 cm² |
| 4 cm | (√3/4) × 16 = 4√3 | 6.928 cm² |
| 6 cm | 9√3 | 15.588 cm² |
| 8 cm | 16√3 | 27.712 cm² |
| 10 cm | 25√3 | 43.30 cm² |
📝 Practice Questions:
Try solving these on your own to master the area of an equilateral triangle:
Q1) Find the area of an equilateral triangle whose side is 12 cm.
Q2) If the area of an equilateral triangle is 100√3 cm², what is the side length?
Q3) An equilateral triangular plot has a side of 20 meters. Find its area.
Q4) A sheet of paper is cut into 3 equilateral triangles with a side of 6 cm each. What is the total area?
Q5) What is the height of an equilateral triangle with area 27√3 cm²?
📚 Answers to Practice Questions:
Q1) Area = (√3 / 4) × 12² = (√3 / 4) × 144 = 36√3 ≈ 62.35 cm²
Q2) Let a² = x
(√3 / 4) × x = 100√3
⇒ x = 400
⇒ a = √400 = 20 cm
Q3) Area = (√3 / 4) × 20² = (√3 / 4) × 400 = 100√3 ≈ 173.2 m²
Q4) Area of one = 9√3
Total = 3 × 9√3 = 27√3 ≈ 46.76 cm²
Q5) Area = ½ × base × height
27√3 = ½ × a × height
Using a = 6 (from earlier)
⇒ 27√3 = ½ × 6 × height
⇒ height = 9√3 ≈ 15.59 cm
🔁 Bonus Trick – Fast Estimation:
Since √3 ≈ 1.732, the shortcut for approximate area:
Area ≈ 0.433 × a²
Helps in quick mental calculation for multiple-choice questions.
📌 Summary Table:
| Topic | Details |
|---|---|
| Type of triangle | Equilateral |
| All sides and angles | Equal (60° each) |
| Area formula | (√3 / 4) × a² |
| Approx formula | 0.433 × a² |
| Derived using | Pythagorean Theorem |
| Application in real life | Architecture, signs, tiling |
| Common exam usage | WBCS, SSC, Railways, UPSC |
✍️ Final Words:
Mastering the area of an equilateral triangle is a stepping stone to excelling in geometry. Once you’re comfortable with the formula, try applying it in tricky word problems and real-life scenarios. Practice is key—so keep solving!
Use the formula regularly, try visualizing the triangle, and don’t forget the shortcut:
Area ≈ 0.433 × side²
**You Might Also Like:
- Must-Know Algebra Formulas for Competitive Exams with Examples & Questions
- Percentage Practice Questions With Answers
- Percentage Formula & Shortcut Tricks for Exams
Download PDF Version
To get a printable “Algebra Formulas for Competitive Exams PDF”, Click Here and revise anytime!