This is one of the most important chapters in quantitative aptitude for competitive exams like SSC, Banking, Railway, UPSC, State PSC, and other government jobs. Even in school and college math, this topic appears in business-related problems.
In this complete guide, we will learn:
- What partnership math means
- Types of partnership
- Important formulas
- Step-by-step solving method
- Solved examples
- Charts and tables for easy understanding
- Practice questions with answers
By the end, you will master the partnership math basic concept and solve any related question confidently.
1. What is Partnership Math?
A partnership is when two or more people join together to run a business. Each partner invests a certain amount of capital (money) for a certain time. At the end of the period, they share the profit or loss based on their contribution.
The basic principle is:
More money invested = bigger share of profit
More time invested = bigger share of profit
2. Types of Partnership in Math:-
In aptitude exams, there are mainly two types of partnerships:
| Type | Explanation | Example |
|---|---|---|
| Simple Partnership | All partners invest their capital for the same period of time. Profit is shared in the ratio of their capitals only. | A invests ₹60,000, B invests ₹40,000 for 1 year → Ratio = 3 : 2 |
| Compound Partnership | Partners invest for different periods. Profit is shared in the ratio of (capital × time). | A invests ₹60,000 for 12 months, B invests ₹40,000 for 8 months → Ratio = (60,000×12) : (40,000×8) |
3. Key Formulas of Partnership Math:-
Let’s go through the important formulas you must know:
(A) Simple Partnership:
If all partners invest for the same duration:
Profit ratio = Capital of A : Capital of B : Capital of C
Example:
A invests ₹80,000, B invests ₹1,20,000 for 1 year.
Ratio = 80,000 : 1,20,000 = 2 : 3.
(B) Compound Partnership:
If partners invest for different times:
Profit ratio = (Capital × Time) of A : (Capital × Time) of B : (Capital × Time) of C
Example:
A invests ₹50,000 for 12 months, B invests ₹40,000 for 9 months.
Ratio = (50,000×12) : (40,000×9) = 600,000 : 360,000 = 5 : 3.
(C) New Partner Joins Later:
When a partner joins after the business has already started:
Profit ratio = (Capital × Time from joining to end)
Example:
A starts with ₹60,000 for 1 year.
B joins after 3 months with ₹80,000.
A = 60,000 × 12 = 720,000
B = 80,000 × 9 = 720,000
Ratio = 1 : 1 → Equal share.
(D) Sleeping Partner:
A sleeping partner only invests money but does not take part in managing the business. Their profit share is still based on capital × time.
4. How to Solve Partnership Math Problems – Step-by-Step:-
Follow these steps for every problem:
- Write down capital and time for each partner.
- If time is in months, keep it in months (no need to convert to years unless necessary).
- Multiply capital × time for each partner.
- Find the ratio of all partners.
- Use this ratio to find each person’s share in profit or loss.
5. Solved Examples – Partnership Math:-
Let’s solve some examples for better understanding.
Example 1 – Simple Partnership:
Q1. A invests ₹60,000 and B invests ₹40,000 for 1 year. Total profit = ₹50,000. Find each partner’s share.
Solution:
Ratio = 60,000 : 40,000 = 3 : 2
A’s share = (3/5) × 50,000 = ₹30,000
B’s share = (2/5) × 50,000 = ₹20,000.
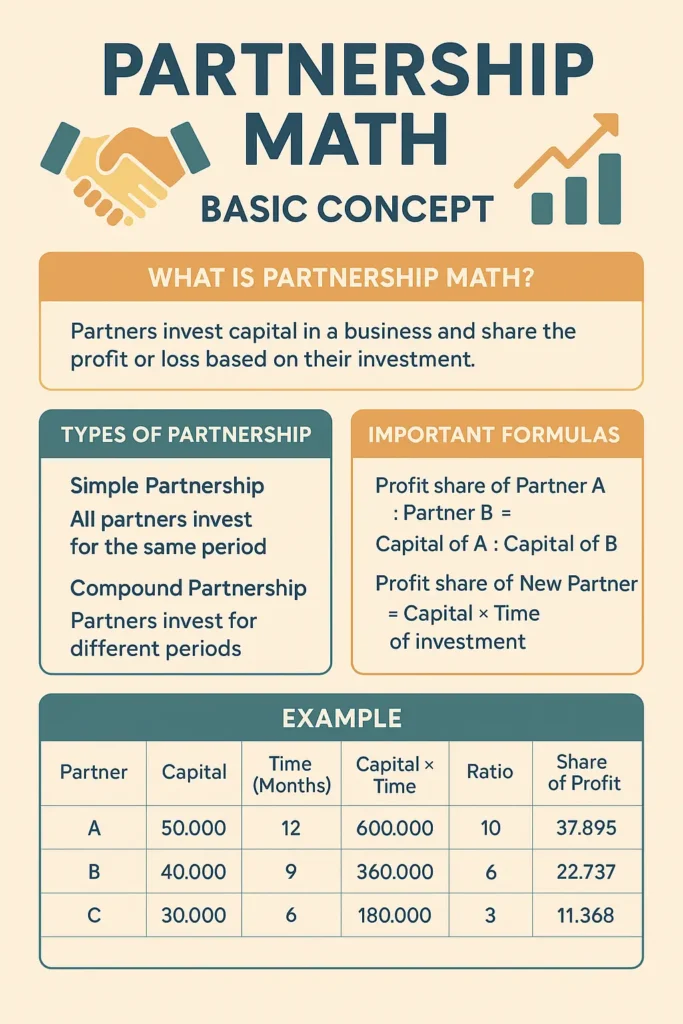
Example 2 – Compound Partnership:
Q2. A invests ₹50,000 for 12 months. B invests ₹40,000 for 9 months. C invests ₹30,000 for 6 months. Total profit = ₹72,000.
Solution:
A = 50,000 × 12 = 600,000
B = 40,000 × 9 = 360,000
C = 30,000 × 6 = 180,000
Ratio = 600,000 : 360,000 : 180,000 = 10 : 6 : 3
Sum = 19
A’s share = (10/19) × 72,000 ≈ ₹37,895
B’s share = (6/19) × 72,000 ≈ ₹22,737
C’s share = (3/19) × 72,000 ≈ ₹11,368
Example 3 – New Partner Joins Later:
Q3. A invests ₹40,000 for 1 year. B joins after 4 months with ₹50,000. Total profit = ₹60,000. Find shares.
Solution:
A = 40,000 × 12 = 480,000
B = 50,000 × 8 = 400,000
Ratio = 480,000 : 400,000 = 6 : 5
A’s share = (6/11) × 60,000 ≈ ₹32,727
B’s share = (5/11) × 60,000 ≈ ₹27,273
6. Quick Reference Chart:-
| Partner | Capital | Time (Months) | Capital × Time | Ratio | Profit Share (₹72,000) |
|---|---|---|---|---|---|
| A | 50,000 | 12 | 600,000 | 10 | ₹37,895 |
| B | 40,000 | 9 | 360,000 | 6 | ₹22,737 |
| C | 30,000 | 6 | 180,000 | 3 | ₹11,368 |
7. Common Mistakes in Partnership Math:-
Students often lose marks because they:
- Ignore time factor in compound partnership.
- Do not convert months correctly.
- Mix up profit ratio with investment ratio.
- Forget to add all ratios before calculating shares.
8. Tips to Solve Partnership Math Fast in Exams:-
- Always calculate capital × time before finding ratio.
- If all partners invest for same time, ignore time.
- Use simplest ratio form to make calculations quicker.
- Practice with previous year exam questions.
9. Practice Questions – Partnership Math:-
Try solving these yourself:
Q1: A invests ₹30,000 for 12 months. B invests ₹40,000 for 8 months. Profit = ₹55,000. Find each share.
Q2: A and B invest ₹50,000 and ₹75,000 for the same period. Profit = ₹1,20,000. Find shares.
Q3: A invests ₹60,000 for 10 months. B invests ₹40,000 for 12 months. C invests ₹50,000 for 8 months. Profit = ₹90,000. Find shares.
Q4: A invests ₹80,000 for 6 months. B joins after 2 months with ₹60,000. Total profit = ₹50,000. Find shares.
10. Answers to Practice Questions:-
A1:
A = 30,000 × 12 = 360,000
B = 40,000 × 8 = 320,000
Ratio = 9 : 8
A’s share = ₹29,118
B’s share = ₹25,882
A2:
Ratio = 2 : 3
A’s share = ₹48,000
B’s share = ₹72,000
A3:
A = 6,00,000
B = 4,80,000
C = 4,00,000
Ratio = 15 : 12 : 10
A’s share ≈ ₹36,486
B’s share ≈ ₹29,189
C’s share ≈ ₹24,324
A4:
A = 80,000 × 6 = 480,000
B = 60,000 × 4 = 240,000
Ratio = 2 : 1
A’s share = ₹33,333
B’s share = ₹16,667
11. Final Thoughts:-
The partnership math basic concept is all about understanding how capital and time together decide the share of profit or loss. Once you know the formulas and follow the step-by-step method, this topic becomes one of the easiest in quantitative aptitude.
With regular practice, you will solve these problems in less than a minute during exams.
So, keep practicing daily and avoid common mistakes. That’s how you will master partnership math and score full marks in this section.
**You Might Also Like:
- Must-Know Algebra Formulas for Competitive Exams with Examples & Questions
- Percentage Important Concepts
- Simple Interest Practice Questions Set 01 – For Govt Job & Academic Exams
Follow Us on Facebook:
Stay updated with the latest math practice sets, tips, and exam strategies. Follow Mathsmine on Facebook for Daily Updates






