What is a Cube Root?
Before jumping to the cube root chart, let’s understand the basic concept.
The cube root of a number is a value that, when multiplied by itself three times, gives the original number.
In simple terms:
If
x = y × y × y,
then
y is the cube root of x.
Example:
The cube root of 8 is 2, because
2 × 2 × 2 = 8
So,
Cube root of 8 = 2
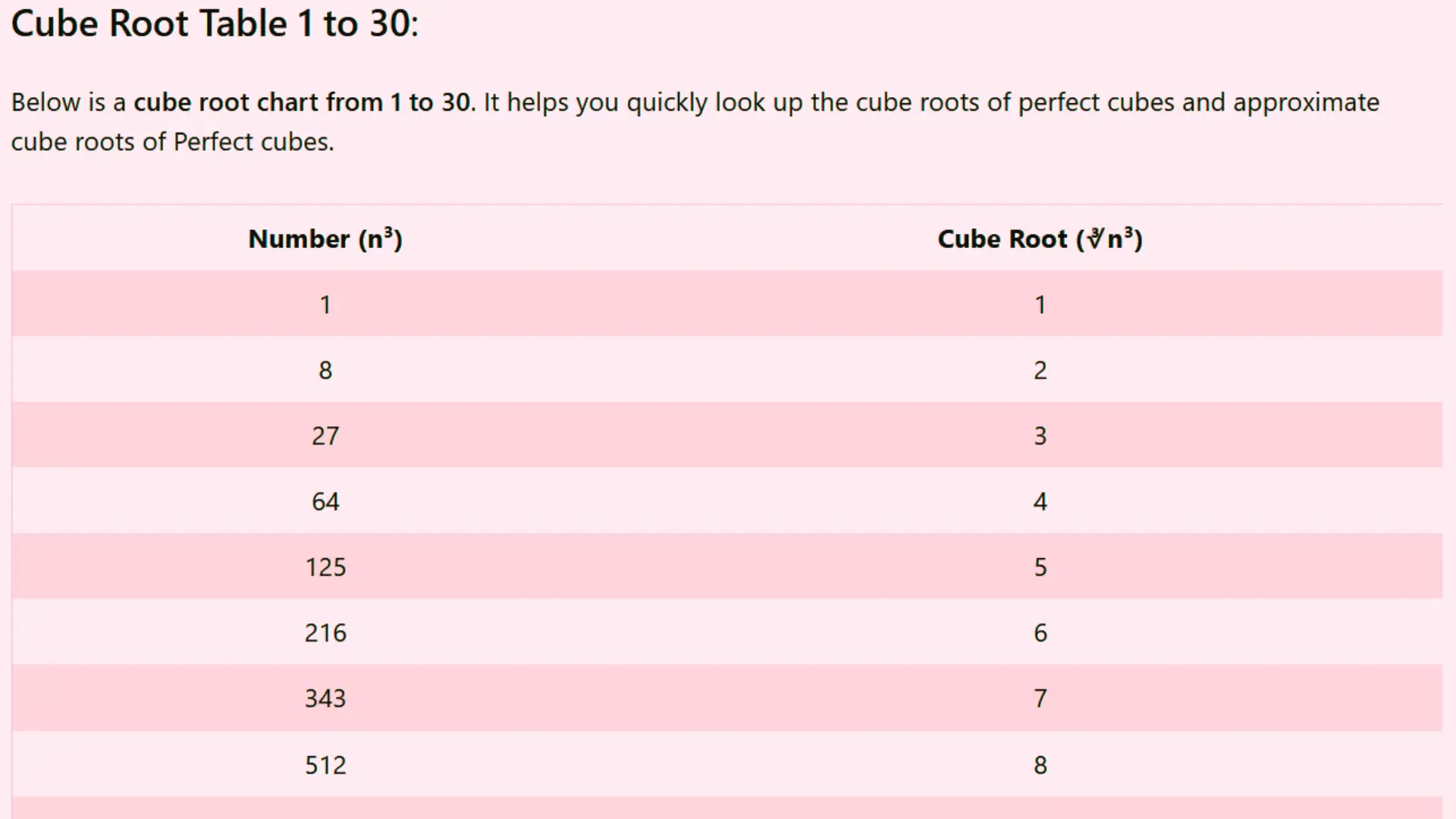
Cube Root Table 1 to 30:
Below is a cube root chart from 1 to 30. It helps you quickly look up the cube roots of perfect cubes and approximate cube roots of Perfect cubes.
| Number (n³) | Cube Root (∛n³) |
|---|---|
| 1 | 1 |
| 8 | 2 |
| 27 | 3 |
| 64 | 4 |
| 125 | 5 |
| 216 | 6 |
| 343 | 7 |
| 512 | 8 |
| 729 | 9 |
| 1000 | 10 |
| 1331 | 11 |
| 1728 | 12 |
| 2197 | 13 |
| 2744 | 14 |
| 3375 | 15 |
| 4096 | 16 |
| 4913 | 17 |
| 5832 | 18 |
| 6859 | 19 |
| 8000 | 20 |
| 9261 | 21 |
| 10648 | 22 |
| 12167 | 23 |
| 13824 | 24 |
| 15625 | 25 |
| 17576 | 26 |
| 19683 | 27 |
| 21952 | 28 |
| 24389 | 29 |
| 27000 | 30 |
Why Use a Cube Root Chart?
A cube root chart is incredibly helpful for:
- Quick lookups during exams
- Estimating roots without a calculator
- Building mental math skills
- Identifying perfect cubes faster
If you’re preparing for competitive exams like SSC, Railways, Banking, or CAT, this chart saves precious time!
Real-Life Applications of Cube Roots:
- Engineering and architecture
- Volume calculations in 3D objects
- Data science (standardizing data)
- Physics formulas
Knowing how to work with a cube root chart gives you an edge in Academics and Competitive Exams.
Solved Examples Using Cube Root Chart:
Example 1: Find ∛27.
Solution: From the cube root chart, ∛27 = 3 (because 3 × 3 × 3 = 27)
Example 2: Estimate ∛20.
Solution: From the chart:
∛20 ≈ 2.714
This is between ∛8 = 2 and ∛27 = 3. So the approximation makes sense.
Example 3: Which number has cube root = 2?
Solution: Cube of 2 = 2³ = 8
So, ∛8 = 2
Practice Questions on Cube Roots:
Try solving these yourself, then check the answers below:
Practice Set:
- Find the cube root of 1.
- Find the cube root of 8.
- Estimate the cube root of 15.
- What is the cube of 4?
- Find the value of ∛27.
Answers:
- ∛1 = 1
- ∛8 = 2
- ∛15 ≈ 2.466 (use cube root chart)
- 4³ = 64
- ∛27 = 3
How to Estimate Cube Roots Mentally (Non-perfect Cubes):
Let’s say you want to find ∛18.
- You know ∛8 = 2 and ∛27 = 3
- 18 lies between 8 and 27
- So, ∛18 lies between 2 and 3
- Closer to 2.6 (check cube root chart for more precision)
Use this mental approximation method for speed.
📥 Download Cube Root Chart PDF (Bonus)
👉 Want a printable version of this cube root chart?
We’ve created a free downloadable cube root table PDF (1 to 30) for your revision and practice– Download Cube Root Chart PDF
Stick it near your study table to revise daily!
Final Words:
The cube root chart 1 to 30 is a powerful tool for math learners. By memorizing perfect cubes and practicing estimations, you can boost your confidence in exams and everyday calculations.
Whether you’re a student or educator, keep this chart handy, solve problems regularly, and keep pushing your math skills further.